Força e movimento – Explicação, exercícios resolvidos – resumo

A força e movimento tem relações diretas. Um corpo só pode ter adquirido movimento se uma força tiver sido aplicada em algum momento. Podemos definir força com uma influência/ação que é capaz de alterar o estado de inércia de um corpo modificando a sua velocidade. O movimento, de forma simples, pode ser definido como a alteração da posição de um corpo em determinado espaço.
Quando um historiador afirma que o movimento social tem força, ele quer dizer que esse movimento pode transformar uma sociedade. Ou seja, dinamizá-la e/ou modificá-la. Quando um estivador ergue uma saca de soja, dizemos que ele é muito forte.
Em Física, nas situações como puxar, empurrar, comprimir, esticar, colocar um corpo em movimento ou em repouso estamos exercendo força.
Neste módulo, estudaremos força, bem como as condições para a existência de movimento.
Definição de força e movimento
O ato de puxar envolve a aplicação de uma força. No cabo de guerra, por exemplo, o grupo que fizer mais força vai arrastar o outro e ganhar a disputa.
Então, você pode ver que forças possibilitam o movimento dos corpos.
Da mesma forma, para que um corpo pare de se movimentar, deve haver a aplicação de uma força.
Além disso, forças podem ser responsáveis pela deformação dos corpos.

Forças são agentes capazes de alterar o movimento dos corpos, aumentando ou diminuindo sua velocidade. As forças também são capazes de deformar os corpos.
Forças são grandezas vetoriais
Parece que o nosso amigo aí ao lado está meio confuso. Imagine que você tivesse perguntado a ele qual o caminho para chegar ao colégio. A resposta teria que vir acompanhada de uma indicação de direção e sentido, pois, sem isso, você não saberia chegar até lá.
É verdade que uma indicação feita como no desenho também não levaria a lugar nenhum; porém; o importante é que você perceba que algumas grandezas físicas são denominadas grandezas vetoriais, isto é, devem ser acompanhadas de indicações de direção e sentido.
As forças fazem parte desse grupo. Elas são grandezas vetoriais e podem ser representadas por vetores, ou seja, por segmentos de reta orientados. Veja:
![]()
Esse vetor nos dá diversas informações sobre a força aplicada ao corpo. Ele nos diz que a força teve direção horizontal, sentido da esquerda para a direita e se estabelecermos uma convenção, por exemplo, de cada centímetro igual a uma unidade de força, veremos que essa força teve intensidade de 6 unidades. No SI, a unidade de força é denominada Newton (N).
Então, temos que esse vetor representa uma força horizontal, da esquerda para a direita, com intensidade de 6N. E podemos escrevê-la por meio de símbolos:
F | = 6N
A descrição da força nos revela alguns elementos que a compõem. Forças possuem direção, que pode ser horizontal, vertical ou inclinada. Cada direção tem dois sentidos: da esquerda para a direita ou da direita para a esquerda, nas forças horizontais. Para cima e para baixo nas forças verticais. E ângulos diversos nas forças inclinadas.

Veja também:
- Acústica – o estudo do som
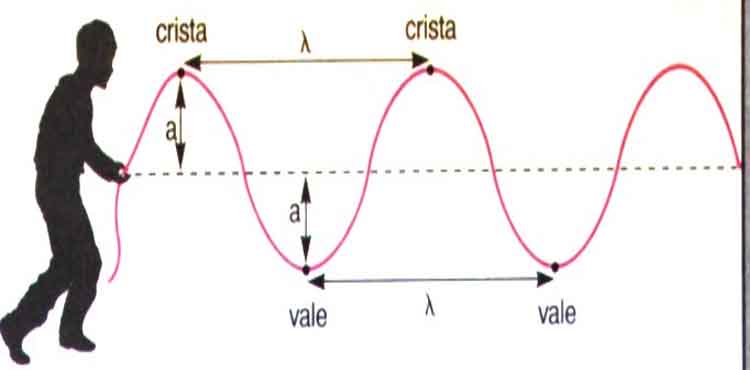
- Movimento ondulatório
- Maquinas Simples: o que são, tipos, exemplos
- Trabalho, potência e energia: fórmulas, resumo e exercícios
- Centro de gravidade e tipos de equilíbrio
- Leis de Newton: exercícios resolvidos, fórmulas – Resumo
- Força e movimento – Explicação, exercícios resolvidos – resumo
- Mecânica Cinemática – Definição exercícios resolvidos aplicação
Sistemas de forças e força resultante
Geralmente, os corpos estão submetidos a mais de uma força, e quando isso acontece, dizemos que eles estão submetidos a um sistema de forças.
No exemplo acima, os índios impulsionam a canoa para frente, o atrito do casco com a água retarda o movimento e a correnteza do rio pode estar ajudando ou atrapalhando o deslocamento.
Porém, em todos os casos, as diversas forças que atuam sobre os corpos podem ser substituídas por uma força única, a resultante (R), que terá o mesmo efeito do sistema.
Cálculo da força resultante
■ Resultante de forças de mesma direção e mesmo sentido
Observe um exemplo desse tipo de sistema: o motorista e seu carona tiveram um problema com o carro durante o trajeto e tiveram que empurrar o veículo. Para isso, ambos fizeram uma força de direção horizontal e mesmo sentido para fazer o carro se movimentar. Poderíamos representar essas forças por vetores:

Então, podemos dizer que a resultante desse sistema será a força de intensidade igual à somatória das duas forças (F1 e F2) aplicadas pelo motorista e seu carona com o mesmo sentido. Isso pode ser representado da seguinte forma:
R = F1 + F2
Admitindo que F1 tenha intensidade de 28N e a F2 seja de 32N, para substituí-las com o mesmo efeito, a resultante terá intensidade de:
R = 28 + 32
R = 60N
■ Resultantes de forças de mesma direção e sentidos contrários
Reveja a ilustração sobre o cabo de guerra: o que acontece ali? Um grupo de pessoas puxa a corda para a esquerda e o outro puxa para a direita. As forças aplicadas têm sentidos diferentes, porém mesma direção, pois todos puxam na horizontal.

E qual será o resultado da disputa? Se a soma das forças que puxam para a direita tiver a mesma intensidade da soma das forças que puxam para a esquerda, ninguém sai do lugar.
Mas, se um dos dois grupos fizer uma força um pouco maior, deslocará os adversários com diferença entre as forças aplicadas.

A resultante terá a direção e sentido da força de maior intensidade. Seu valor será a diferença entre as duas.
R = F1 – F2
Admitindo que o homem (F1) esteja exercendo uma força de intensidade 33N e o bode (F2) também exerça uma força de 33N, a resultante será zero, pois não há deslocamento nem do homem, nem do bode.
R = 33 – 33
R = 0
Mas, se o bode diminuir a intensidade de sua “teimosia”, e passar a exercer uma força de 31N, o que irá acontecer?
Teremos:
R = 33 – 31
R = 2N
O bode será arrastado pelo homem com intensidade de 2N.
■ Forças que formam um ângulo no ponto de aplicação
Veja o exemplo que segue. Nele você pode notar que duas forças atuam sobre o corpo formando um ângulo entre elas.
Nesse caso, a resultante pode ser encontrada usando a regra do paralelogramo, isto é, encontraremos a resultante fazendo uso de um desenho geométrico.
Para isso, partindo da extremidade da F2 traçamos uma paralela à F1 e da extremidade de F1 traçamos uma paralela à F2. A resultante será a diagonal que sai do ponto de aplicação do paralelogramo formado.
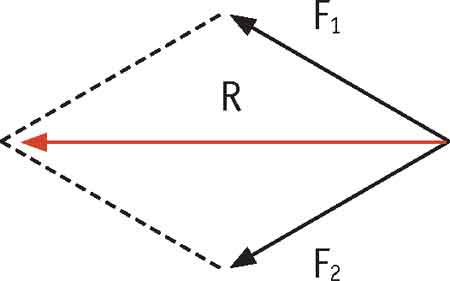
Quando o ângulo formado pelas forças for diferente de 90° faremos a determinação da resultante apenas pela regra do paralelogramo. Mas, quando o ângulo for igual a 90°, podemos calcular a resultante aplicando o Teorema de Pitágoras. Veja:
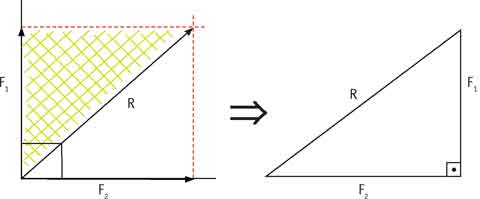
Ao fazermos o traçado da perpendicular do paralelogramo, podemos observar que surgem dois triângulos retângulos.
Vamos analisar o triângulo. Nele, os catetos correspondem à projeção da F1 e da F2, e a hipotenusa é a própria resultante. Relembrando o que nos diz o Teorema de Pitágoras (o quadrado da hipotenusa é igual à soma dos quadrados dos catetos), temos que:
R2 = F12 + F12
Exemplificando:
Se F1 tiver intensidade de 3N e F2 de 4N, a resultante das duas será:
R2= 32 + 42
R2 = 9 + 16
R2 = 25
R = √25
R = 5N
Questão resolvida
- Considerando um corpo qualquer, represente, por meio de vetores, algumas forças que a ele são aplicadas:
a) Força de 3N aplicada verticalmente, de cima para baixo.
b) Força de 7N aplicada horizontalmente da direita para a esquerda.
c) Força de 4N aplicada verticalmente de baixo para cima.
Solução:

Sugestão de atividades – Exercícios
- A respeito dos mesmos sistemas do exercício 1, calcule a resultante de cada um.
- Determine a resultante de três forças, sabendo que duas atuam no sentido leste e têm intensidades de 706N e 338N e a outra age no sentido oeste e tem intensidade de 1 076N.
- Determine a intensidade da resultante de duas forças de 6N e 8N, que fazem um ângulo reto no ponto de aplicação.
- Em uma brincadeira de cabo de guerra, duas equipes de quatro crianças estão na disputa. A equipe A tem seus membros puxando para a direita, com forças de 12N, 14N, 16N e 13N, a equipe B tem seus membros puxando para a esquerda e fazendo forças de 11N, 14N, 16N e 15N.
a) Qual a intensidade total das forças exercidas pela equipe A?
b) Qual a intensidade total das forças exercidas pela equipe B?
6. Trace a força resultante dos sistemas abaixo:

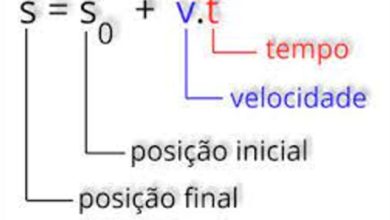

NAO ENTENDI A 6
Na sugestão de atividades a questão 1 está sem sentido.
Eu entendi que a força é como uma ação que é capaz de alterar o estado de inércia de um corpo modificando a sua velocidade, como um movimento de forma simples, que pode ser definido como a alteração da posição de um corpo em determinado espaço.