Conjuntos numéricos e teoria dos conjuntos

Os conjuntos numéricos estão presentes em muitos aspectos da vida, sejam eles cotidianos, culturais ou científicos. Por exemplo, formamos conjuntos ao organizar a lista de amigos para uma festa agrupar os dias da semana ou simplesmente fazer grupos.

Os componentes de um conjunto são chamados de elementos. Para enumerar um conjunto usamos geralmente uma letra maiúscula.

Representações Pode ser definido por: -Enumerando todos os elementos do conjunto: S={1, 3, 5, 7, 9} -Simbolicamente: B={x∈ N|x<8}, enumerando esses elementos temos: B={0,1,2,3,4,5,6,7}

Diagrama de Venn

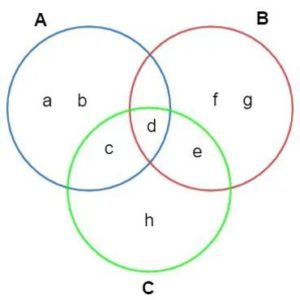
Há também um conjunto que não contém elemento e é representado da seguinte forma: S=∅ ou S={ }.

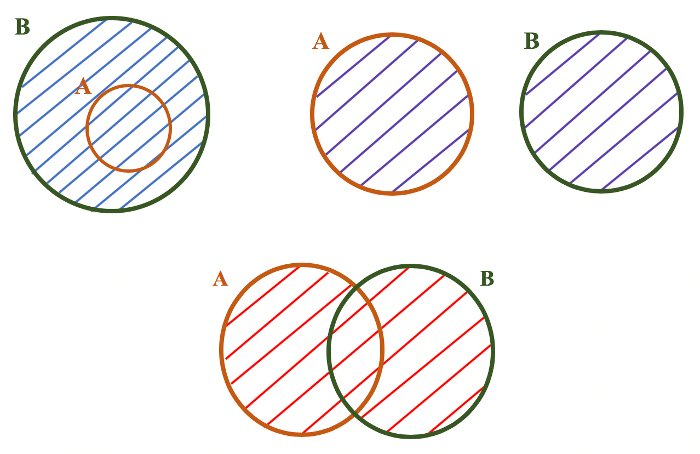
Quando todos os elementos de um conjunto A pertencem também a outro conjunto B, dizemos que:

• A é subconjunto de
• Ou A é parte de B
• A está contido em B escrevemos: A⊂B

Se existir pelo menos um elemento de A que não pertence a B: A⊄B

Igualdade: Propriedades básicas da igualdade

Para todos os conjuntos A, B e C, para todos os objetos x ∈ U, temos que:

(1) A = A.

(2) Se A = B, então B = A.

(3) Se A = B e B = C, então A = C.

(4) Se A = B e x ∈ A, então x∈ B.

Se A = B e A ∈ C, então B ∈ C.

Dois conjuntos são iguais se, e somente se, possuem exatamente os mesmos elementos. Em símbolo:

A=B se, e somente se,∀x(x∈A↔x∈B).

Para saber se dois conjuntos A e B são iguais, precisamos saber apenas quais são os elementos.

Não importa ordem:
A={1,2,3} e B={2,1,3}

Não importa se há repetição:
A={1,2,2,3} e B={1,2,3}

Tipos de Operações

União

Dados dois conjuntos A e B, existe sempre um terceiro formado pelos elementos que pertencem pelo menos um dos conjuntos a que chamamos conjunto união e representamos por: A∪B.

Formalmente temos: A∪B={x|x∈A ou x∈B}. Exemplo:

A={1,2,3,4} e B={5,6}
A∪B={1,2,3,4,5,6}

Interseção

A interseção dos conjuntos A e B é o conjunto formado pelos elementos que são ao mesmo tempo de A e de B, e é representada por : A∩B. Simbolicamente: A∩B={x|x∈A e x∈B}

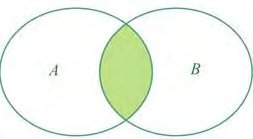
Exemplo:
A={a,b,c,d,e} e B={d,e,f,g}
A∩B={d,e}

Diferença

Uma outra operação entre conjuntos é a diferença, que a cada par A, B de conjuntos faz corresponder o conjunto definido por:

A – B ou A\B que se diz a diferença entre A e B ou o complementar de B em relação a A.

A este conjunto pertencem os elementos de A que não pertencem a B.

A\B = {x : x∈A e x∉B}.

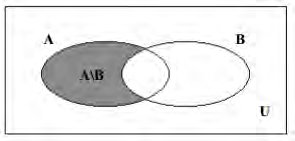
Exemplo:
A = {0, 1, 2, 3, 4, 5} e B = {5, 6, 7}

Então os elementos de A – B serão os elementos do conjunto A menos os elementos que pertencerem ao conjunto B.

Portanto A – B = {0, 1, 2, 3, 4}.

Exercícios

1 – CÂMARA DE SÃO PAULO/SP – TÉCNICO ADMINISTRATIVO – FCC/2014) Dos 43 vereadores de uma cidade, 13 dele não se inscreveram nas comissões de Educação, Saúde e Saneamento Básico. Sete dos vereadores se inscreveram nas três comissões citadas. Doze deles se inscreveram apenas nas comissões de Educação e Saúde e oito deles se inscreveram apenas nas comissões de Saúde e Saneamento Básico. Nenhum dos vereadores se inscreveu em apenas uma dessas comissões. O número de vereadores inscritos na comissão de Saneamento Básico é igual a:

A) 15.

B) 21.

C) 18.

D) 27.

E) 16.

2 – (ESPCEX – CADETES DO EXÉRCITO – EXÉRCITO BRASILEIRO/2013) Uma determinada empresa de biscoitos realizou uma pesquisa sobre a preferência de seus consumidores em relação a seus três produtos: biscoitos cream cracker, wafer e recheados. Os resultados indicaram que:

– 65 pessoas compram cream crackers.

– 85 pessoas compram wafers.

– 170 pessoas compram biscoitos recheados.

– 20 pessoas compram wafers, cream crackers e recheados.

– 50 pessoas compram cream crackers e recheados.

– 30 pessoas compram cream crackers e wafers.

– 60 pessoas compram wafers e recheados.

– 50 pessoas não compram biscoitos dessa empresa.

Determine quantas pessoas responderam essa pesquisa.

A) 200

B) 250

C) 320

D) 370

E) 530

3 – O diagrama indica a distribuição de atletas da delegação de um país nos jogos universitários por medalha conquistada. Sabe-se que esse país conquistou medalhas apenas em modalidades individuais. Sabe-se ainda que cada atleta da delegação desse país que ganhou uma ou mais medalhas não ganhou mais de uma medalha do mesmo tipo (ouro, prata, bronze). De acordo com o diagrama, por exemplo, 2 atletas da delegação desse país ganharam, cada um, apenas uma medalha de ouro.

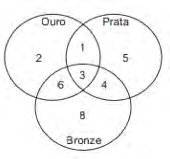
A análise adequada do diagrama permite concluir corretamente que o número de medalhas conquistadas por esse país nessa edição dos jogos universitários foi de:

A) 15.

B) 29.

C) 52.

D) 46.

E) 40.

Respostas

1. RESPOSTA: “C”.

APENAS 12 se inscreveram em educação e saúde (o 12 não deve ser tirado de 7 como costuma fazer nos conjuntos, pois ele já desconsidera os que se inscreveram nos três)

APENAS 8 se inscreveram em saúde e saneamento básico.

São 30 vereadores que se inscreveram nessas 3 comissões, pois 13 dos 43 não se inscreveram.

Portanto, 30-7-12-8=3

Se inscreveram em educação e saneamento 3 vereadores.

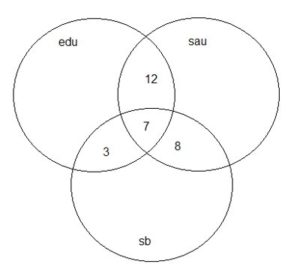
Só em saneamento se inscreveram: 3+7+8=18

---

2. RESPOSTA: “B”.

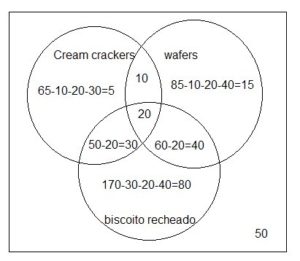
5+10+15+20+30+40+80+50=250 pessoas

 

---

3. RESPOSTA: “D”.

O diagrama mostra o número de atletas que ganharam medalhas.

No caso das intersecções, devemos multiplicar por 2 por ser 2 medalhas e na intersecção das três medalhas multiplica-se por 3.

Intersecções:

6 ∙ 2 = 12

1 ∙ 2 = 2

4 ∙ 2 = 8

3 ∙ 3 = 9

Somando as outras: 2+5+8+12+2+8+9=46

---

Veja também

• O que são maquinas simples
• Estrutura Atômica: estrutura do átomo – partículas – resumo
• Tabela Periódica completa – Elementos químicos
• O que são Ligações Químicas – Distribuição Eletrônica

Bibliografia

• BARBOSA, Rafael. E. P. L. Utilizando a tecnologia para o aprimoramento da cognição matemática: recursos multimídia aplicados à educação matemática. Disponível em: http://www.feg.unesp.br/entidades/rePET/29.pdf. Acesso em: 29 mar. 2012.
• DOLCE, Osvaldo; POMPEO, José Nicolau. Fundamentos de matemática elementar: geometria plana. 8. ed. São Paulo: Atual, 2005. v. 9.